FUNCIONES TRIGONOMÉTRICAS. SENO, COSENO Y TANGENTE.

-TRIÁNGULOS RECTÁNGULOS

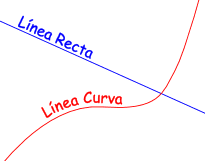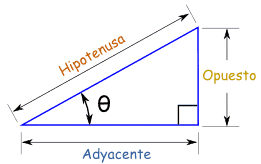
(Adyacente significa tocando el ángulo, y opuesto es opuesto al ángulo...)

SENO, COSENO Y TANGENTE.

Función seno:	sin(θ) = Opuesto / Hipotenusa
Función coseno:	cos(θ) = Adyacente / Hipotenusa
Función tangente:	tan(θ) = Opuesto / Adyacente

TEOREMAS PARA LOS ÁNGULOS EN LOS TRIÁNGULOS

1.- Teorema para ángulos internos:
 Los ángulos internos de cualquier triángulo suman 180°.

2.- Teorema para un ángulo externo:
 Todo ángulo externo de un triángulo es igual a la suma de los ángulos interiores no adyacentes.

3.- Teorema para ángulos externos:
 La suma de los ángulos externos de cualquier triángulo es igual a 360°.

RECTAS Y PUNTOS NOTABLES

 En el triángulo podemos obtener 4 puntos notables y 4 rectas notables, dependiendo de la recta que obtengamos será el punto notable del triángulo.
-Rectas Notables:
1.- Bisectriz
2.- Mediatriz
3.- Altura
4.- Mediana

-Puntos Notables:
1.- Incentro: Es el punto de intersección de las 3 bisectrices de los ángulos interiores del triángulo. El incentro es el centro de la circunferencia inscrito en el triángulo.


2.- Circuncentro: Es el puno de intersección de las mediatrices de los lados de triángulos, el circuncentro es el centro de la circunferencia circunscrita en el triángulo.

3.- Ortocentro: Alturas. El ortocentro es un punto donde se cortan las 3 alturas de un triángulo.

4.- Baricentro: Es el punto donde se cortan las 3 medianas de los triángulos, es decir es el punto donde está aplicado todo el peso de un cuerpo triangular por lo que es su centro de gravedad.

TRIÁNGULOS

TRIÁNGULO:
Figura geométrica de 3 lados.
Sus 3 ángulos suman 180º.
3 vértices.

CLASIFICACIÓN:
Isóseles: Dos lados iguales y uno desigual.
Equilátero: Tres lados iguales.
Escaleno: Tres lados desiguales.

CLASIFICACIÓN POR MEDIO DE LOS ÁNGULOS:
Triángulo Rectángulo: Sí tiene un ángulo recto.


Triángulo Obtusángulo: Un ángulo obtuso (mas de 90º) y 2 ángulos agudos (menos de 90º)


Triángulo Acutángulo: Tres ángulos agudos (menos de 90º)

DETERMINACIÓN DE LA ALTURA POR TEOREMA DE TALES

APRENDIZAJE ESPERADO:

Establece la relación de semejanza de triángulos en el Teorema de Tales.
Aplica el Teorema de Tales en el cálculo de alturas y longitudes.
Formula resultados aplicando el Teorema de Tales.


DETERMINACIÓN DE LA ALTURA POR MEDIO DEL TEOREMA DE TALES:
 Cuando miramos alrededor o salimos a dar un paseo en especial por nuestra ciudad, apreciamos en cada paso que damos la cantidad de cosas que representan figuras o formas geométricas sean regulares o irregulares. El conocimiento geométrico básico es indispensable para desenvolverse en nuestra vida cotidiana para orientarse reflexivamente en el espacio, como para hacer estimaciones de alturas, distancias aveces inaccesibles. Tal es el caso que podemos calcular la altura de monumentos, edificios, piedras enormes, etc.



TEOREMA DE TALES EN UN TRIÁNGULO:
 Se dice que dos triángulos están en posición de Tales si, tienen en común un ángulo y los lados opuestos a éste ángulo común en cada triángulo son paralelos.

EL AXIOMA, POSTULADO, TEOREMA Y COROLARIO

AXIOMA: Un axioma es una proposición que e considera "evidente"y se acepta sin requerir demostración previa. Es un sistema hipotético-deductivo, es toda proposición no deducida (de otras) si no que se constituye una regla general de pensamiento gráfico.

POSTULADO: Un postulado es una proposición no evidente por sí misma ni demostrada, pero que se acepta ya que no existe otro principio del que pueda ser deducida.

COROLARIO: Un corolario es un término que se utiliza en matemáticas y en lógica para designar la evidencia de un teorema o de una definición ya demostrados, sin necesidad de invertir un esfuerzo adicional en su demostración.

TEOREMA: Un teorema es una proposición que afirma una verdad demostrable. En matemáticas, es toda proposición que partiendo de un supuesto hipótesis afirma una verdad.

UNIDAD DE MEDIDA ACTUAL

 MEDIR UN SEGMENTO ES COMPARARLO CON OTRO ELEGIDO COMO UNIDAD. PARA ÉSTE FIN SE USAN LAS UNIDADES DE LONGITUD DEL SISTEMA MÉTRICO DECIMAL O DEL SISTEMA INGLÉS.
 LOS INSTRUMENTOS DE MEDICIÓN USADOS EN LA ACTUALIDAD SON: REGLA, METRO FLEXÓMETRO, CINTA MÉTRICA, ESCUADRA, ESCALÍMETRO.

TABLA DE CONVERSIONES

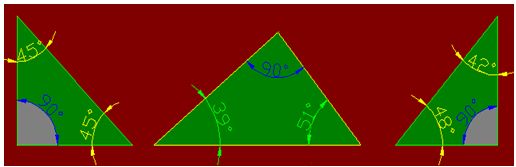
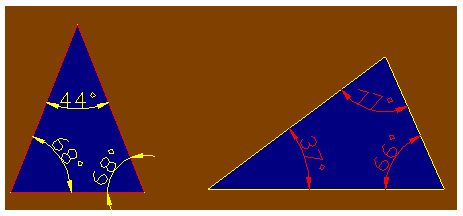
UNIDAD	CM	M	PULGADA	PIE	YARDA
1 centímetro	1	0.01	0.3937	0.032808	0.010936
1 metro	100	1	39.37	3.2808	1.0936
1 pulgada	2.54	0.0254	1	0.083333	0.027778
1 pie	30.48	0.3048	12	1	0.33333
1 yarda	91.44	0.9144	36	3	1

MAGNITUD	SISTEMA	ABREVIACIÓN	UNIDAD	SÍMBOLOS
-LONGITUD	Metro-Kilogramo-Segundo	MKS	Metro	m
-LONGITUD	Centímetro-Gramo-Segundo	CKS	Centímetro	cm
-LONGITUD	SISTEMA INGLÉS	SI	Pulgada	Plg o in

UNIDADES DE MEDIDA ANTIGUAS

Codo	El hombre utilizó inicialmente alguna parte de su cuerpo, por ejemplo el codo, que una unidad muy mencionada en la biblia
	Dedo	El dedo equivalía al ancho real, aproximadamente: 18 mm.
	Mano	La mano equivalía al ancho de la mano, aun se usa en algunos países para maedir la alzada de un caballo.
	Pie	Esta medida vale: 30,5cm. y se usa para medir por ejemplo las chapas de los techos
	Cuarta	Se extiende o abre la mano y la medida entre la punta del pulgar y el meñique equivale a un palmo o cuarta(ver figura)
	Braza	Equivale a 1.67 m. y es el resultado de extender ambos brazos
	Cable	Es una unidad utilizada para estimar la distancia entre dos objetos poco alejados, equivale a 120 brazas, es decir, unos 200 m.
	Vara	En España valía 0,84 m. y en Argentina 0.866.
	Pulgada	Medida inglesa y vale, luego de un acuerdo internacional: 2.54 cm. Muy usada actualmente.
	Pertiga	Vale entre 16 y 22 pies, según la zona donde se utilice.
	Linea	Corresponde a la 1/12 parte de la pulgada
	Paso	Equivale a la medida entre un pie y el próximo, al efectuar un paso
	Milla	Deriva de mille passuum y signifca unos 1000 pasos.

ELEMENTOS BÁSICOS DE LA GEOMETRÍA

PUNTO: Un punto geométrico es imaginado tan pequeño que carece de dimensiones. La representación de puntos geométricos se caracteriza por la huella que deja un lápiz bien afilado sobre el papel.

LÍNEA: Es un conjunto de puntos continuos que nos permite distinguir dos lìneas que son lìnea recta y línea curva.

LÍNEA RECTA: Es aquella que tiene sus dos puntos en una misma dirección.

LÍNEA CURVA: Es la que está generada por una continuidad de puntos que cambian de dirección frecuentemente.


SEMI RECTA O RAYO: Conjunto de puntos formados por al "A" y todos los que le siguen o preceden.


SEGMENTO: Conjunto de puntos comprendidos entre "A" y "B", más esos dos puntos denominados extremos del segmento.

SEGMENTO ORIENTADO (VECTOR): Es todo segmento que cuenta con dirección y magnitud. Un vector no tiene una ubicación definida; puede trasladarse a cualquier parte del plano sin modificar ni su módulo, ni su orientación (dirección y sentido).


SEGMENTO CONSECUTIVO: Se define como segmento consecutivo al que tiene un extremo en común.


LÍNEA QUEBRADA O POLIGONAL: Lìnea compuesta de segmentos contínuios que siguen diferentes direcciones.


CURVA SIMPLE CERRADA: Es aquella que al trazarse empieza y termina en un mismo punto.


POLIGONAL SIMPLE CERRADA: Es aquella que al trazarse con lìneas quebradas termina y empieza en el mismo punto.


SUPERFICIE: Es un conjunto de puntos de un espacio.

PLANO: Una superficie como una pared, el piso, la cubierta de una mesa, los espejos, forman un plano, en geometría el plano no tiene límites por su extensión, pero para representarlo se hace a través de un paralelogramo que muestre su posición.

CUERPO GEOMÉTRICO: Un  cuerpo geométrico es una figura geométrica de tres dimensiones: largo, ancho y alto.

ANTECEDENTES HISTÓRICOS DE LA GEOMETRÍA

ETAPAS DE LA GEOMETRÍA

Según escritos encontrados a lo largo de la historia de la humanidad, los hechos más importantes referidos a la ciencia de la Geometría apuntan a las culturas de los babilonios, egipcios y los griegos.

Sumerios-Babilonios

Las culturas que se desarrollaron alrededor de los ríos Tigris y Éufrates de la antigua Mesopotamia fueron los sumerios, acadios, asirios y babilonios; en base a las necesidades de resolver antiguos problemas comunes, ya calculaban áreas de algunas figuras geométricas, como el rectángulo y el triángulo; se les atribuye la invención de la rueda y la obtención del grado sexagesimal como proceso de dividir la circunferencia en 360 partes iguales, establecieron las primeras aproximaciones de pi. mediante la relación numérica entre diámetro y su circunferencia.

Egipcios

Debido a que la población vivió prácticamente en los márgenes del río Nilo, su principal actividad fué la agricultura, uno de los problemas que enfrentaron fue los desbordamientos de los ríos en época de lluvia por lo que literalmente arrasaba con las tierras de cultivo y que constantemente tenías que realizar medidas de perímetros y áreas para delimitar sus parcelas con la finalidad de calcular el nuevo pago de impuestos que debían hacer como dueños del terreno, de aquí que Geometría provenga del vocablo griego Geo (tierra) y metría (medida) y que significa medidas de tierras, así que prácticamente se le atribuye el descubrimiento de la geometría a la raíz de este fenómeno.Además calcularon áreas de triángulos como el isóseles, el trapecio y círculo así como volúmenes de poliedros como el caso de las pirámides; dieron un valor aproximado para pi es igual a 3.1604, como herramienta de medición característica de esa fecha surge el cordel como regla y compás para la construcción y diseño de las pirámides.

Griegos

Los primeros tratados formales de la geometría datan de la época de Tales de Mileto; famoso por su teorema de las rectas paralelas y por haber hecho las primeras aproximaciones de las alturas de las pirámides de Egipto mediante la proporcionalidad entre los lados de los triángulos semejantes, fundó la escuela Jónica distinguiéndose entre los discípulos más destacados Pitágoras de Samus famoso por su teorema del triángulo rectángulo.

Otro personaje famoso fué Arquímedes de Siracusa quién descubrió diversas formas de medir la superficie de algunas figuras curvas, así como el área y el volúmen de sólidos limitados por superficies curvas como los cilindros, aunque sobresalieron otros personajes famoso por sus contribuciones, sin duda el personaje considerado por algunos como el que le dió un órden lógico a todas las aportaciones de la Geometría fué Euclides de Alejandría quién escribió la obra cumbre llamada "Los Elementos" y que consiste en 13 tomos o volúmenes considerados como la base de la geometría elemental o euclidiana, dichos manuscritos contiene todas las contribuciones en órden lógico compuestos por toda la base axiomática, sus postulados, teoremas y lemas.