TRIÁNGULOS

TRIÁNGULO:
Figura geométrica de 3 lados.
Sus 3 ángulos suman 180º.
3 vértices.

CLASIFICACIÓN:
Isóseles: Dos lados iguales y uno desigual.
Equilátero: Tres lados iguales.
Escaleno: Tres lados desiguales.

CLASIFICACIÓN POR MEDIO DE LOS ÁNGULOS:
Triángulo Rectángulo: Sí tiene un ángulo recto.


Triángulo Obtusángulo: Un ángulo obtuso (mas de 90º) y 2 ángulos agudos (menos de 90º)


Triángulo Acutángulo: Tres ángulos agudos (menos de 90º)

DETERMINACIÓN DE LA ALTURA POR TEOREMA DE TALES

APRENDIZAJE ESPERADO:

Establece la relación de semejanza de triángulos en el Teorema de Tales.
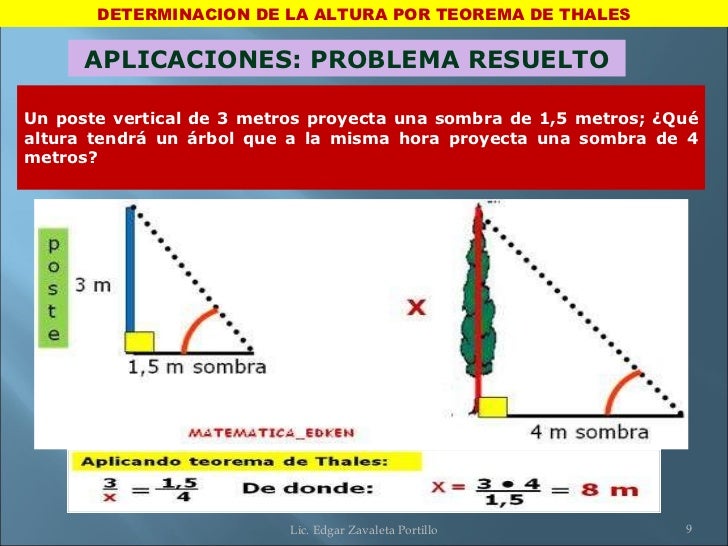
Aplica el Teorema de Tales en el cálculo de alturas y longitudes.
Formula resultados aplicando el Teorema de Tales.


DETERMINACIÓN DE LA ALTURA POR MEDIO DEL TEOREMA DE TALES:
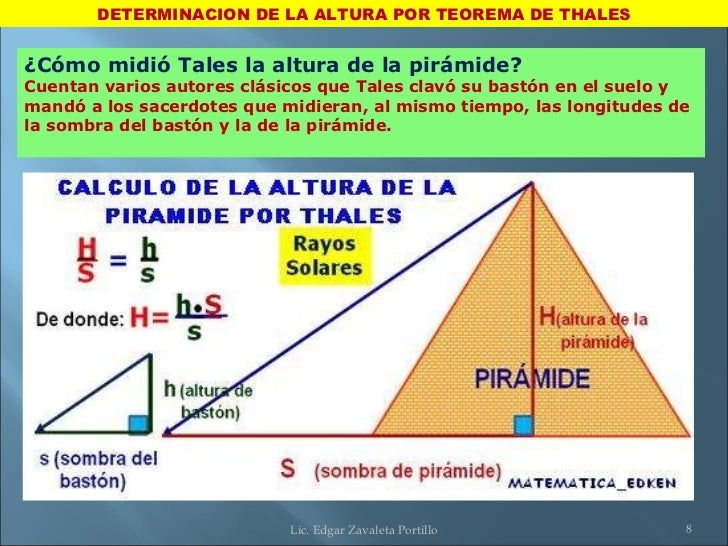
 Cuando miramos alrededor o salimos a dar un paseo en especial por nuestra ciudad, apreciamos en cada paso que damos la cantidad de cosas que representan figuras o formas geométricas sean regulares o irregulares. El conocimiento geométrico básico es indispensable para desenvolverse en nuestra vida cotidiana para orientarse reflexivamente en el espacio, como para hacer estimaciones de alturas, distancias aveces inaccesibles. Tal es el caso que podemos calcular la altura de monumentos, edificios, piedras enormes, etc.



TEOREMA DE TALES EN UN TRIÁNGULO:
 Se dice que dos triángulos están en posición de Tales si, tienen en común un ángulo y los lados opuestos a éste ángulo común en cada triángulo son paralelos.