FUNCIONES TRIGONOMÉTRICAS. SENO, COSENO Y TANGENTE.

-TRIÁNGULOS RECTÁNGULOS

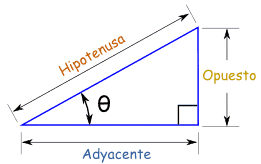
(Adyacente significa tocando el ángulo, y opuesto es opuesto al ángulo...)

SENO, COSENO Y TANGENTE.

Función seno:	sin(θ) = Opuesto / Hipotenusa
Función coseno:	cos(θ) = Adyacente / Hipotenusa
Función tangente:	tan(θ) = Opuesto / Adyacente

TEOREMAS PARA LOS ÁNGULOS EN LOS TRIÁNGULOS

1.- Teorema para ángulos internos:
 Los ángulos internos de cualquier triángulo suman 180°.

2.- Teorema para un ángulo externo:
 Todo ángulo externo de un triángulo es igual a la suma de los ángulos interiores no adyacentes.

3.- Teorema para ángulos externos:
 La suma de los ángulos externos de cualquier triángulo es igual a 360°.

RECTAS Y PUNTOS NOTABLES

 En el triángulo podemos obtener 4 puntos notables y 4 rectas notables, dependiendo de la recta que obtengamos será el punto notable del triángulo.
-Rectas Notables:
1.- Bisectriz
2.- Mediatriz
3.- Altura
4.- Mediana

-Puntos Notables:
1.- Incentro: Es el punto de intersección de las 3 bisectrices de los ángulos interiores del triángulo. El incentro es el centro de la circunferencia inscrito en el triángulo.


2.- Circuncentro: Es el puno de intersección de las mediatrices de los lados de triángulos, el circuncentro es el centro de la circunferencia circunscrita en el triángulo.

3.- Ortocentro: Alturas. El ortocentro es un punto donde se cortan las 3 alturas de un triángulo.

4.- Baricentro: Es el punto donde se cortan las 3 medianas de los triángulos, es decir es el punto donde está aplicado todo el peso de un cuerpo triangular por lo que es su centro de gravedad.

TRIÁNGULOS

TRIÁNGULO:
Figura geométrica de 3 lados.
Sus 3 ángulos suman 180º.
3 vértices.

CLASIFICACIÓN:
Isóseles: Dos lados iguales y uno desigual.
Equilátero: Tres lados iguales.
Escaleno: Tres lados desiguales.

CLASIFICACIÓN POR MEDIO DE LOS ÁNGULOS:
Triángulo Rectángulo: Sí tiene un ángulo recto.


Triángulo Obtusángulo: Un ángulo obtuso (mas de 90º) y 2 ángulos agudos (menos de 90º)


Triángulo Acutángulo: Tres ángulos agudos (menos de 90º)

DETERMINACIÓN DE LA ALTURA POR TEOREMA DE TALES

APRENDIZAJE ESPERADO:

Establece la relación de semejanza de triángulos en el Teorema de Tales.
Aplica el Teorema de Tales en el cálculo de alturas y longitudes.
Formula resultados aplicando el Teorema de Tales.


DETERMINACIÓN DE LA ALTURA POR MEDIO DEL TEOREMA DE TALES:
 Cuando miramos alrededor o salimos a dar un paseo en especial por nuestra ciudad, apreciamos en cada paso que damos la cantidad de cosas que representan figuras o formas geométricas sean regulares o irregulares. El conocimiento geométrico básico es indispensable para desenvolverse en nuestra vida cotidiana para orientarse reflexivamente en el espacio, como para hacer estimaciones de alturas, distancias aveces inaccesibles. Tal es el caso que podemos calcular la altura de monumentos, edificios, piedras enormes, etc.



TEOREMA DE TALES EN UN TRIÁNGULO:
 Se dice que dos triángulos están en posición de Tales si, tienen en común un ángulo y los lados opuestos a éste ángulo común en cada triángulo son paralelos.

EL AXIOMA, POSTULADO, TEOREMA Y COROLARIO

AXIOMA: Un axioma es una proposición que e considera "evidente"y se acepta sin requerir demostración previa. Es un sistema hipotético-deductivo, es toda proposición no deducida (de otras) si no que se constituye una regla general de pensamiento gráfico.

POSTULADO: Un postulado es una proposición no evidente por sí misma ni demostrada, pero que se acepta ya que no existe otro principio del que pueda ser deducida.

COROLARIO: Un corolario es un término que se utiliza en matemáticas y en lógica para designar la evidencia de un teorema o de una definición ya demostrados, sin necesidad de invertir un esfuerzo adicional en su demostración.

TEOREMA: Un teorema es una proposición que afirma una verdad demostrable. En matemáticas, es toda proposición que partiendo de un supuesto hipótesis afirma una verdad.

UNIDAD DE MEDIDA ACTUAL

 MEDIR UN SEGMENTO ES COMPARARLO CON OTRO ELEGIDO COMO UNIDAD. PARA ÉSTE FIN SE USAN LAS UNIDADES DE LONGITUD DEL SISTEMA MÉTRICO DECIMAL O DEL SISTEMA INGLÉS.
 LOS INSTRUMENTOS DE MEDICIÓN USADOS EN LA ACTUALIDAD SON: REGLA, METRO FLEXÓMETRO, CINTA MÉTRICA, ESCUADRA, ESCALÍMETRO.

TABLA DE CONVERSIONES

UNIDAD	CM	M	PULGADA	PIE	YARDA
1 centímetro	1	0.01	0.3937	0.032808	0.010936
1 metro	100	1	39.37	3.2808	1.0936
1 pulgada	2.54	0.0254	1	0.083333	0.027778
1 pie	30.48	0.3048	12	1	0.33333
1 yarda	91.44	0.9144	36	3	1

MAGNITUD	SISTEMA	ABREVIACIÓN	UNIDAD	SÍMBOLOS
-LONGITUD	Metro-Kilogramo-Segundo	MKS	Metro	m
-LONGITUD	Centímetro-Gramo-Segundo	CKS	Centímetro	cm
-LONGITUD	SISTEMA INGLÉS	SI	Pulgada	Plg o in